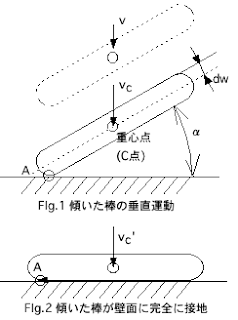
初心に戻って少し復習

たわみ量の話題が続いていたので、次に作用する力についても計算をやっていきたい、というノリなのだが、その前に少し復習をしてみたいと思う。

どのような作業でもそうだが、実際取り組もうとしている事柄を事前にイメージしてから、作業すると「よく考えてみれば当たり前だった」というような簡単なミスをなくすことに繋がる。また、いきなり、難しい式を並べ立てると、私自身、何をやっているのか段々と分からなくなってくる性格であるので、難しく考えすぎず、まず大体のイメージを理解したいと思う。そこで、定式化を行う前に、まず、シンプルなモデルにおいて、どのような速度、加速度波形になるか、想像してイメージして十分捉えてから、定式化作業に入りたいと思う。

まず、図1 のような問題を考えてみた。
地面に置かれている物体(剛体)が、後ろから、ポンッと押されて、移動した後、地面との摩擦によって停止するモデルだ。地面との摩擦というと、なにか、難しいような気がしてくるのだが、振動の教科書に記載されるような一般化モデルで表現すると、図2 のように表現できると思う。（ただし物体は返ってこないので、バネ定数項はゼロ）

図1.

図2.

これは、実際に、テーブルに消しゴムなどを置いて指で、はじいている感じを想像すれば良いのだと思う。初速度ゼロの物体は、押されて、速度が上昇し暫くした後、最高速度に達する。その後、また速度は低下し、速度ゼロになって停止するといった具合になると、私はイメージする。最高速度が 3.0 [m/sec] で、移動時間が、3.0 [sec] であった場合を例にとって考えると、以下の図3 のような感じになると思う。尚、時間のズレであるとか、停止における速度低下の方が、もっと緩やかであるとか、色々と細かな違いは、実際にはあると思う。

図3.

速度を表現できれば、あとは、それを微分して加速度。また積分して変位量を表現することが出来るので、加速度、変位量波形も、上の図3に記載してみた。

ここで、平均速度(図3 内では、Average Velocity)という値がある。これは、以下の式によって求められる。
平均速度 = 結果として移動した距離 / 移動時間
上の図3には、この平均速度というのも記載してみた。
今回の場合、移動距離が 4.5 [m] 移動時間が 3.0 [sec] としたので
平均速度 = 4.5 / 3.0 = 1.5 [m/sec] となる。
これは、図3を見たら分かる通り、速度が一定であったと仮定した場合の、速度値になる。しかし、実際にはこのような速度変化の様子は不可能ではあると思う。ここで、思い出したいのだが、力は、加速度に比例する。
F = m ⋅ a
加速度は、速度の時間あたりの変化で、速度一定であるなら、当然加速度はゼロとなる。速度一定と取り扱うと、加速度はゼロとなり、力もゼロということになってしまう。

よって、速度は一定値ではなく、時間あたりに変化していく関数（変数,変動する数値）という捉え方で定式化を行わなければ、力を求めることは出来ないということになる。

また、力が最大となるのは、速度が最大となる時間とはズレることに気づいた。まぁ、当たり前のことであったのだが、速度が上昇している途中（加速中）の途中で最大を迎える。


次に、よくある問題として、ボールの落下という現象を考えてみた。図4。

図4.

落下中、ボールは、一定の重力加速度によって等加速度運動を行う。ボールが接地後、地面から跳ね返されるまでは、ボール自身の弾力、または、地面の弾力性によって支配されるバネ・マス系の振動モデルに近い状態となる。ここで、地面との反発係数が１で、減衰は起きなかったと仮定すると、ボールが地面から跳ね返された後の速度は、ボールが接地したときの最高速度と同じで、方向がまったく反対となる。
上のことをふまえて、地面との接地までにかかる時間が 3.0[sec] , 接地中の時間が 3.0[sec](接触時間) と仮定した時の、速度波形を想像すると、図5のようになると思う。(下方向の運動を、マイナス方向としてある)

図5.

また、速度波形を微分して加速度波形、積分して変位波形も記載してみた。

まぁ、これも当たり前のことではあるが、加速度波形から分かる通り、力が最大となるのは、ボールの移動量が最大となった時であることが分かる。

また、ボール自体を弾性体と見なした上で、ボールの下部表面点を、速度の測定点と捉えた場合は、以下の図6 のようになることに注意したい。

図6.

接地している間中、ボールの下部表面点は、速度がゼロとなるので、加速度もまたゼロとなる。これでは、また力を求めることはできない。きちんと、その運動する物体が持つ質量に相当する点（重心点）を速度測定点として捉える必要がある。
尚、ボール自体を剛体とみなし、地面が変形すると捉える場合は、ボールの何処を測定しても、速度は同じであるので、ボールにおける速度測定点を何処に定義しても問題はない。

ボールの重心点については、変形前では、確かにボールの中心座標である。しかし、地面との接地後、ボールが変形している様子を図5では、上下対称形状が保たれると仮定した上で図示しているが、実際の変形している過程において、この仮定条件が完全に当てはまることは考えにくい。また、ボールの変形する、その過程において、その都度、どの位置が重心点であるのか、それを測定することは、困難であるということは容易に予想がつく。

これら、上でイメージしてみた波形を頭に入れた後、力を求める為の定式化にのぞもうと思う。次から、これらの波形のイメージ自身が、合致しているのかどうかも含めて、ある運動を行う物体に作用する力を求める方法について整理していく。

Impactをもっと使ってみる3

Fig.1 のように、質量 m の剛体が、v₀の一定速度で、運動しているとします。
剛体が、長さ L , 断面積 A の棒に衝突したとき、棒はどの程度たわむ（圧縮）ことになるか、求めてみようと思います。

ただし、棒自身の質量による、慣性力（静止していようとする慣性力）は無視するとします。また、剛体が、棒に衝突した瞬間から、剛体は棒と一体となって運動する（跳ね返りは無かった）ものとします。

剛体の運動エネルギーを、棒の弾性歪みエネルギーで、完全に吸収したとした（剛体の運動が静止し、棒のたわみ量が最大となった）と考えます。

剛体が速度 v₀ で運動している場合、剛体が持っている運動エネルギーは、
1 / 2 ⋅ ( m ⋅ v₀² )

バネ定数 k のバネが、x だけ縮むとき、その弾性歪みエネルギーは、
1 / 2 ⋅ ( k ⋅ x² )

ここで、棒の軸方向に荷重 F を加えた時の、たわみ量 x を求める式は、
x = ( F ⋅ L ) / ( A ⋅ E )

上式を、F= となるように整理すると、
F = ( ( A ⋅ E ) / L ) ⋅ x
となる。
上式と、フックの法則式 F = k ⋅ x を比較すると、ちょうどバネ定数 k に相当する部分がわかる。よって、長さ L , 断面積 A , 縦弾性係数 E の棒を考えた場合、そのバネ定数 k は、
k = ( ( A ⋅ E ) / L )
となる。

よって、バネの弾性歪みエネルギーの式より、棒の弾性歪みエネルギーは、
1 / 2 ⋅ ( k ⋅ x² ) = 1 / 2 ⋅ ( ( ( A ⋅ E ) / L ) ⋅ x² )

今、剛体の運動エネルギーを、棒の弾性歪みエネルギーで、完全に吸収したときを考えているので、
1 / 2 ⋅ ( m ⋅ v₀² ) = 1 / 2 ⋅ ( ( ( A ⋅ E ) / L ) ⋅ x² )
となる。

よって、棒の軸方向たわみ量 x は、
x = √( m ⋅ v₀² ⋅ L / ( A ⋅ E ) )
となるはず。


次に、たわみが最大となる時間について考えてみる。
Fig.3 のように、バネ⋅マス系と捉えると、これは周期的な振動をする１自由度系の振動モデルと捉えることができる。このような単純な１自由度系の振動モデルの、固有円振動数 ω_n [rad/sec] は、

ω_n = √( k / m )

ここで、バネ定数 k は、Fig.1 のような棒の場合、k = ( ( A ⋅ E ) / L ) と表現することができるので、固有円振動数 ω_n [rad/sec] は、以下のように書き直せる。

ω_n = √( ( ( A ⋅ E ) / L ) ⋅ 1 / m )


右図のような振動周期(sin波)を考えた場合、たわみ量（圧縮）が最大となる時間は、1/4 周期の時であることが分かる。
よって、たわみ量（圧縮）が最大となる時間 t [sec] は、π / 2 [rad] を、その固有円振動数 ω_n [rad/sec] で割ったもの、

t = ( π / 2 ) ⋅ ( 1 / ω_n ) [sec]

となるはず。

今、棒の縦弾性係数 E = 1000 [Pa] , 全長 L = 100 [m] , 直径 D = 2.0 [m] の棒と、剛体の質量 m = 10 [kg] , 初速度 v₀ = 1.0 [m/sec] の剛体を考えると、
棒のたわみ量は、
x = √( 10.0 × 1.0² × 100.0 / ( ( 1.0² × π ) × 1000.0 ) ) = 0.5642 [m]

棒のたわみ量（圧縮）が最大となる時間は、
ω_n = √( ( ( ( 1.0² × π ) × 1000.0 ) / 100.0 ) × 1 / 10.0 ) = 1.77245 [rad/sec]
t = ( π / 2 ) × ( 1 / 1.77245 ) = 0.8862 [sec]

以前までのブログ記事と同様に、上のような Impact FEM 用モデルを作成し、同様な条件で、速度 v₀ で運動している剛体（質点）を、棒に衝突させてみた。

Fig.4 剛体（質点）の速度

Fig.5 棒 先端部の たわみ量

まず、棒のたわみ量が最大となる（剛体の速度がゼロとなる）時間は、0.8831 [sec] (理論式との差異 0.35 [%]) となった。また、その際の、棒のたわみ量は、0.5626 [m] (理論式との差異 0.28 [%]) であった。

ここで、注意点がある。理論式では棒自身の質量は無視しているが、陽解法では、振動の伝播を扱うので、質量密度がゼロの物体は、計算ができない（振動しない）。ここでは、結果に対して十分寄与が小さくなるだけの小さな質量密度を棒に与えた。そのため、若干ではあるが、棒自身の質量によって、静止しようとする慣性力（抵抗力）が発生し、それにより、理論式よりも たわみ量は小さくなるはずである。Impact FEM による計算結果は、その予測通りであった。

上までは、エネルギーの保存則によって、たわみ量を求めてきたが、物体の運動を表現するに、エネルギーという値の他に運動量というものがある。運動量には、それに関わる法則として「運動量の変化は、力積に等しい。」というものがある。さらに詳しく言うと、力が一定値でなく時間と共に変化している関数である場合は、F-t グラフを作成した場合の、その面積（積分,総和）と、運動量の変化は等しい。
今回の計算においても「運動量の変化は、力積に等しい。」が成立しているのかどうか見てみようと思う。

上の問題では、質量 m = 10 [kg] , 初速度 v₀ = 1.0 であったので、棒のたわみ量が最大となる時間での、運動量の変化量は、

m ⋅ v₀ - m ⋅ v = 10.0 × 1.0 - 10.0 × 0.0 = 10.0

次に、今回の計算において、棒に作用している力 F と、時間 t のグラフは、以下のようになっていた。

Fig.6 棒に作用している荷重

上記のグラフデータを、時間0 ~ 0.8831 で区間積分（台形則による数値積分）を行ったところ、その力積(面積)は、10.001 であった。

理論式と、陽解法プログラムによる結果と、どちらも理論上での数値同士の比較ではあるが、たしかに、運動量の変化は、力積に等しいことを見ることができた。

Impactをもっと使ってみる2

物体の運動方程式（運動量の保存則）の理解を深めるために、以下のような問題について、理論式と解析の比較を行ってみた。以下の問題は、陰解法と陽解法による非線形構造解析の実際に記載してある問題を、そのまま使わせて頂いています。

傾いた棒(長さ l , 質量 m)が、壁面に向かって、ある速度でもって運動していくとき、壁面との接地点(A点)での跳ね返りは無かったと仮定すると、右図のような運動をする。(Fig.1 から Fig.2 の状態に、棒は運動する)

壁面との衝突後に、棒が回転しながら運動する速度 v_c' を求めてみる。

棒は衝突直前までは、速度v_c でもって、並進方向に運動していく。角運動量 L = r × m ⋅ v より、壁との接地点(A点)での角運動量で整理すると、

L_A = r × m ⋅ v = l / 2 × m ⋅ (v_c cosα)

ただし、棒の幅寸法については、その寸法値は十分小さいもので、結果に対しても影響が小さいと仮定し、無視(幅寸法 -> ゼロ)してある。

次に、衝突直後について整理する。壁面との摩擦が０であると仮定すると、壁面から及ぼされる衝撃力は、壁面から垂直上方向となる。よって、棒の速度方向は、その方向を変えることなく、新たな速度 v_c' でもって運動を継続する。また、壁面との接地点(A点)が、壁面上で左方向に滑る運動が付け加わる為、棒は回転運動をすることになる。ここで、棒の回転運動の角速度を仮に ω' とする。ある慣性モーメント I_rod を持つ物体が、角速度 ω' で運動するとき、その角運動量は、L = I_rod ⋅ ω' と表現できる。
よって、衝突後での棒の角運動量は、

L_A' = ( r × m ⋅ v ) + ( I_rod ⋅ ω' ) = ( l / 2 × m ⋅ (v_c' cosα) ) + ( I_rod ⋅ ω' )

ここで、角運動量の保存則より、

L_A = L_A'

が成り立つ。

上に述べた式から整理していくと、v_c' を求める式が得られる。
ここで、 I_rod , ω' についても、既知の数値(棒の長さ,棒の質量,v_c' , α) で、表現してやる必要があるが、実際やってみると、これが結構長い手順であったので、このブログ記事では割愛する。結果だけであるが、v_c' を求める式は、以下のようになる。

v_c' = 3 v_c ⋅ ( cos²α / (1 + 3 ⋅ cos²α) )

衝突直前までの棒の速度 v_c を 1.0 [m/sec] , 棒の傾き角度 α を 30 度 とすると、v_c' は、

v_c' = 3.0 × 1.0 × ( cos²(30) / (1 + 3 × cos²(30) ) ) = 0.6923 [m/sec]

上記のような棒のモデルを、Impact FEM 用に作成し、同様な条件で、速度 v_c を与え、壁面から跳ね返りがないように衝突させてみた。

Fig.3 壁面に接地後の様子

Impact FEM は陽解法プログラムであるので、解が振動しているが、速度値 v_c' は、大体 0.701 [m/sec] の値に収束している。理論式で得られた数値との差異は、1.26 [%] で、かなり近い値が得られた。

Impact FEM では、剛体が定義された節点郡に対して、さらに境界条件としての拘束などを与えることが困難なため、棒は、十分剛と思われる程度の剛性を定義した弾性体とした∗1。そのため、棒自体の変形によって、若干のエネルギ散逸（変形エネルギ散逸）が起こる。また理論式では、棒の幅寸法について無視したとことで、三角関数を用いた成分計算のときの角度値が、真値とは少しずれている。これらの要因から、理論式とは少し数値がずれているものと考える。

∗1 : ここでは、致し方なく十分剛な弾性体を使用したが、十分剛な弾性体を、陽解法で計算するモデル内に含むと、安定時間増分 Δt を無意味に縮小させ、計算コストを増大させるので、あまり好ましくない方法ではある。また、剛に近い弾性体による、妙な高周波ノイズを結果に含むことにもなる。なまじ、陰解法より、実際の現象に忠実な解法であるため、実際には存在し得ない剛体などという定義の扱いに、特に注意しないといけない気がする。

Impactをもっと使ってみる

前回、Impactで単純な棒波の計算を実施して理論との比較とかいう ややこしいことをしてましたが、いかんせん、形が単純すぎて現実感がない。やはり、おもしろさをもっと向上するためには、現実感があり、目で見て触れて感じれるぐらいのものが良いような感じがしたので、形だけでも車らしくした、下のような計算をしたりしてました。

このモデルは、Blenderで作りました。
たしかに、これぐらいの形状を表現してくると、見栄えはよく現実感みたいなものが得られるんですが、うちの iBook G4 では、計算時間が大変かかるようになってきて、なかなか結果を鑑賞することが出来ない問題がでてきました。陽解法での、衝突計算は、Δt との戦いみたいですね。
ちなみに、この、Impactは、接触問題をペナルティ法によって解いてるようです。このペナルティ法のクセと、あとΔtの取り方を理屈ではなく経験によって理解度を向上させるのに、このImpactの利用は、大変有益でした。

ペナルティ法って、接触体の間に、バネを発生させて、あたかも接触しているような変形をそれぞれの接触面に発生させる方法ですが、あたかも当たっているような状態であって、当たっている状態 とは違う。当然あたかも当たっているような状態なだけで、当たっているとは認識されていないので、間に発生させているバネ力より、接触面間の運動による力の方が勝れば、突き抜けていくモードになるんですね。実際には、どんだけ力が大きくなっても当たっている限りは、破壊でもしない限り貫通なんてことは起きないんですけど。あと、接触間に見えないバネを作るということで、バネは弾性体なので、接触間の見えない要素（バネ）によって、エネルギが散逸されてしまう という実際には無いエネルギ散逸現象が付け加わるデメリットもあるみたいですね。短い計算時間で接触問題を解く良い手法なんですが、なんでもかんでも良いものなってなかなか無いですね。

物体内の波動伝播

物体内の波動の伝播を表現する式は、要素のタイプによって異なるが、ビーム（棒）要素の場合の伝播速度は、c = √(E / ρ) で表されるらしい。ここで、Eは縦弾性係数、ρは質量密度。これは、物体内を振動波が伝播していく速度を表現したもので、空気をその媒介物として考えた場合、音速を表現したものとも言える。
ところで、物体内の伝播速度が上記であるとした場合、例えば、長さ=L の棒があった場合、その先端から波動が入力されて、反対側まで到達する為の時間は、time = L / c 。 また、反対側から波動が跳ね返って先端に返ってくる時間もまた、time = L / c 。 ということで、棒に波動を与えて変形させた場合、その波動が、また先端まで返ってくるまでの総時間は、time_total = 2L / c となるはず。
ここで、有限要素法の解法の一つである陽解法では、運動方程式による陽関数によって変形モードが算出される解法で、波動の伝播を扱う問題について、良好な精度を示すということを聞いた。そこで、陽解法で解くフリーソフト Implact Finite Element Program を使って棒に波動を与えた場合に、波動が跳ね返ってくる時間を計算してみることにした。
モデルは、SI単位系で統一し、長さL=100[m]、直径=2.0[m] の棒(Rod_2) 。波動の速度を計算しやすくするために、縦弾性係数E=1000[Pa] , 質量密度&rho=0.1[kg/m³] の材料特性。それに、初速度1.0[m/sec] の衝撃速度（棒の圧縮方向）を与えてみた。物体内の波動伝播速度は、c = 100 [m/sec] となるので、先端にまで跳ね返ってくる時間は、time_total = 2 * 100 / 100 = 2.0 [sec] となるはず。

Implact Finite Element Programで計算を実施し、棒の先端部の変位量をプロットしたグラフを右に示す。グラフを見ると、圧縮して変形した棒が、時間1.0[sec]で、圧縮しきって次に変形が元に戻りはじめ、時間2.0[sec]には変位0に戻っていることがわかる。減衰は考慮しない材料特性としたので、波動は減衰せず、さらに棒は伸びていく変形になり、また伸びきった後、縮んでいく変形が繰り返されることになった。
近頃、静的な問題（陰解法）から、衝突現象の問題に触れる機会が多くなってきた。実際の衝突の事象を考えると、大きな変形や接触によって入力方向が絶えず変化し複雑なもので、理解しがたいところがある。そのため、得られた結果（試験、計算機）を鵜呑みにし、その推測（仮説）と考察を怠っていた所があった。改善すべき事象と改良すべき部位の理解を深めていくため、まずは１軸方向に入力方向を固定した問題を解いてみたのだが、単純問題であれば推測した期待通りの解が、アニメーションと計算結果値で見れた。このことで、少し波動の考え方が分かった気がする。少し嬉しい気持ちというか、なんというか不思議な気持ちになった。
今更というかなんというか、ここで少しおもしろかったのが、波動が跳ね返ってくるまでの時間に、その速度（波動の大きさ）が関係しないという点だった。もちろん、最大変位量は、増減するのだが、棒の変位が０となるまでの時間に対して、速度を変化させても影響がなかった。まぁ、知っている人は当然知っていることなのであろうが、私にとっては、ちょっとした発見でした。

- 2007/4/16 : グラフの Y軸ラベル の単位が間違っていたので修正しました。

Gmsh

Gmsh の新しいバージョンv2.0 がリリースされているようです。（情報おそい）
起動してすぐのぱっとみた感じ、すぐにはどこが変わってるのかよくわからなかったんですが、よく見たら、ファイルの読み込み(Open)可能なファイル形式欄に、STEP , IGES , BREP のCADファイル形式が追加されていました。なにげに、持っていたSTEPファイルを読み込んでみたのですが、読み込んで開きましたよ。これはビックリ。
これで、CADシステムで作った形状データを書き出して、Gmshに読み込んでMeshを生成し、計算に持ち込んで遊ぶといったことができそうです。以前までは、CADデータを読み込むことが出来なかったので、demo ファイを読み込んでみたり、シンプルなデータをGmsh上で作ってみて、ちまちまと遊んでみたりといったことしか出来なかったので、活用の場面があまり想像できなく残念だったんですが、これで色々な使い道が考えられそうです。
でも、Gmsh上で 読み込んだ後のGeometry の編集作業は難しそう。そうすると、３次元CADが、すぐ近くに欲しい気になってきます。なにか、機能制限付きCADとかで、フリーライセンスのCADないですかね。

コメントについて

今日、BloggerをBeta版から、正式版にUpgradeした。そうすると、「未確認の投稿」というものがハイライトされていました。そこを見ると、私のBlogに対して２件のコメントがあることを知らせていました。
しかし、公開しているブログを見ても、0 commentsのまま。どうやら、このBlogの管理者が承認しないとコメントも表示されない設定にしてしまっていたようでした。そのため、たまに、ログインせずにブログを表示して下にあるコメント数を見ていたのですが、0 commentsとなっていて、コメントを頂いていることに気づいていませんでした。コメント書いて頂いた方、投稿に気づかず放置状態となっていて、すみませんでした。