くまＢｌｏｇ

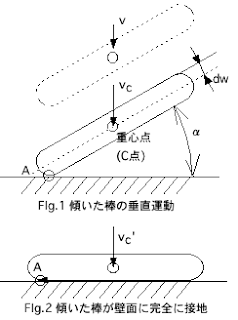
物体の運動方程式（運動量の保存則）の理解を深めるために、以下のような問題について、理論式と解析の比較を行ってみた。以下の問題は、 陰解法と陽解法による非線形構造解析の実際 に記載してある問題を、そのまま使わせて頂いています。 傾いた棒(長さ l , 質量 m)が、壁面に向かって、ある速度でもって運動していくとき、壁面との接地点(A点)での跳ね返りは無かったと仮定すると、右図のような運動をする。(Fig.1 から Fig.2 の状態に、棒は運動する) 壁面との衝突後に、棒が回転しながら運動する速度 v c ' を求めてみる。 棒は衝突直前までは、速度v c でもって、並進方向に運動していく。角運動量 L = r × m ⋅ v より、壁との接地点(A点)での角運動量で整理すると、 L A = r × m ⋅ v = l / 2 × m ⋅ (v c cosα) ただし、棒の幅寸法については、その寸法値は十分小さいもので、結果に対しても影響が小さいと仮定し、無視(幅寸法 -> ゼロ)してある。 次に、衝突直後について整理する。壁面との摩擦が０であると仮定すると、壁面から及ぼされる衝撃力は、壁面から垂直上方向となる。よって、棒の速度方向は、その方向を変えることなく、新たな速度 v c ' でもって運動を継続する。また、壁面との接地点(A点)が、壁面上で左方向に滑る運動が付け加わる為、棒は回転運動をすることになる。ここで、棒の回転運動の角速度を仮に ω' とする。ある慣性モーメント I rod を持つ物体が、角速度 ω' で運動するとき、その角運動量は、L = I rod ⋅ ω' と表現できる。 よって、衝突後での棒の角運動量は、 L A ' = ( r × m ⋅ v ) + ( I rod ⋅ ω' ) = ( l / 2 × m ⋅ (v c ' cosα) ) + ( I rod ⋅ ω' ) ここで、角運動量の保存則より、 L A = L A ' が成り立つ。 上に述べた式から整理していくと、v c ' を求める式が得られる。 ここで、 I rod , ω' についても、既知の数値(棒の長さ,棒の質量,v c ' , α) で、表現し

前回、 Impact で単純な棒波の計算を実施して理論との比較とかいう ややこしいことをしてましたが、いかんせん、形が単純すぎて現実感がない。やはり、おもしろさをもっと向上するためには、現実感があり、目で見て触れて感じれるぐらいのものが良いような感じがしたので、形だけでも車らしくした、下のような計算をしたりしてました。 このモデルは、 Blender で作りました。 たしかに、これぐらいの形状を表現してくると、見栄えはよく現実感みたいなものが得られるんですが、うちの iBook G4 では、計算時間が大変かかるようになってきて、なかなか結果を鑑賞することが出来ない問題がでてきました。陽解法での、衝突計算は、Δt との戦いみたいですね。 ちなみに、この、 Impact は、接触問題をペナルティ法によって解いてるようです。このペナルティ法のクセと、あとΔtの取り方を理屈ではなく経験によって理解度を向上させるのに、この Impact の利用は、大変有益でした。 ペナルティ法って、接触体の間に、バネを発生させて、あたかも接触しているような変形をそれぞれの接触面に発生させる方法ですが、 あたかも当たっているような状態 であって、 当たっている状態 とは違う。当然 あたかも当たっているような状態 なだけで、 当たっている とは認識されていないので、間に発生させているバネ力より、接触面間の運動による力の方が勝れば、突き抜けていくモードになるんですね。実際には、どんだけ力が大きくなっても 当たっている 限りは、破壊でもしない限り貫通なんてことは起きないんですけど。あと、接触間に見えないバネを作るということで、バネは弾性体なので、接触間の見えない要素（バネ）によって、エネルギが散逸されてしまう という実際には無いエネルギ散逸現象が付け加わるデメリットもあるみたいですね。短い計算時間で接触問題を解く良い手法なんですが、なんでもかんでも良いものなってなかなか無いですね。

物体内の波動の伝播を表現する式は、要素のタイプによって異なるが、ビーム（棒）要素の場合の伝播速度は、c = √(E / ρ) で表されるらしい。ここで、Eは縦弾性係数、ρは質量密度。これは、物体内を振動波が伝播していく速度を表現したもので、空気をその媒介物として考えた場合、音速を表現したものとも言える。 ところで、物体内の伝播速度が上記であるとした場合、例えば、長さ=L の棒があった場合、その先端から波動が入力されて、反対側まで到達する為の時間は、time = L / c 。 また、反対側から波動が跳ね返って先端に返ってくる時間もまた、time = L / c 。 ということで、棒に波動を与えて変形させた場合、その波動が、また先端まで返ってくるまでの総時間は、time total = 2L / c となるはず。 ここで、有限要素法の解法の一つである陽解法では、運動方程式による陽関数によって変形モードが算出される解法で、波動の伝播を扱う問題について、良好な精度を示すということを聞いた。そこで、陽解法で解くフリーソフト Implact Finite Element Program を使って棒に波動を与えた場合に、波動が跳ね返ってくる時間を計算してみることにした。 モデルは、SI単位系で統一し、長さL=100[m]、直径=2.0[m] の棒(Rod_2) 。波動の速度を計算しやすくするために、縦弾性係数E=1000[Pa] , 質量密度&rho=0.1[kg/m 3 ] の材料特性。それに、初速度1.0[m/sec] の衝撃速度（棒の圧縮方向）を与えてみた。物体内の波動伝播速度は、c = 100 [m/sec] となるので、先端にまで跳ね返ってくる時間は、time total = 2 * 100 / 100 = 2.0 [sec] となるはず。 Implact Finite Element Program で計算を実施し、棒の先端部の変位量をプロットしたグラフを右に示す。グラフを見ると、圧縮して変形した棒が、時間1.0[sec]で、圧縮しきって次に変形が元に戻りはじめ、時間2.0[sec]には変位0に戻っていることがわかる。減衰は考慮しない材料特性としたので、波動は減衰せず、さらに棒は伸びていく変形になり、また伸びきった後、縮んでいく変形が繰り返されるこ