Impactをもっと使ってみる2
物体の運動方程式(運動量の保存則)の理解を深めるために、以下のような問題について、理論式と解析の比較を行ってみた。以下の問題は、陰解法と陽解法による非線形構造解析の実際に記載してある問題を、そのまま使わせて頂いています。
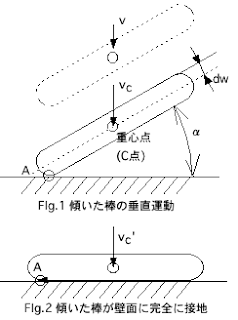
傾いた棒(長さ l , 質量 m)が、壁面に向かって、ある速度でもって運動していくとき、壁面との接地点(A点)での跳ね返りは無かったと仮定すると、右図のような運動をする。(Fig.1 から Fig.2 の状態に、棒は運動する)
壁面との衝突後に、棒が回転しながら運動する速度 vc' を求めてみる。
棒は衝突直前までは、速度vc でもって、並進方向に運動していく。角運動量 L = r × m ⋅ v より、壁との接地点(A点)での角運動量で整理すると、
LA = r × m ⋅ v = l / 2 × m ⋅ (vc cosα)
ただし、棒の幅寸法については、その寸法値は十分小さいもので、結果に対しても影響が小さいと仮定し、無視(幅寸法 -> ゼロ)してある。
次に、衝突直後について整理する。壁面との摩擦が0であると仮定すると、壁面から及ぼされる衝撃力は、壁面から垂直上方向となる。よって、棒の速度方向は、その方向を変えることなく、新たな速度 vc' でもって運動を継続する。また、壁面との接地点(A点)が、壁面上で左方向に滑る運動が付け加わる為、棒は回転運動をすることになる。ここで、棒の回転運動の角速度を仮に ω' とする。ある慣性モーメント Irod を持つ物体が、角速度 ω' で運動するとき、その角運動量は、L = Irod ⋅ ω' と表現できる。
よって、衝突後での棒の角運動量は、
LA' = ( r × m ⋅ v ) + ( Irod ⋅ ω' ) = ( l / 2 × m ⋅ (vc' cosα) ) + ( Irod ⋅ ω' )
ここで、角運動量の保存則より、
LA = LA'
が成り立つ。
上に述べた式から整理していくと、vc' を求める式が得られる。
ここで、 Irod , ω' についても、既知の数値(棒の長さ,棒の質量,vc' , α) で、表現してやる必要があるが、実際やってみると、これが結構長い手順であったので、このブログ記事では割愛する。結果だけであるが、vc' を求める式は、以下のようになる。
vc' = 3 vc ⋅ ( cos2α / (1 + 3 ⋅ cos2α) )
衝突直前までの棒の速度 vc を 1.0 [m/sec] , 棒の傾き角度 α を 30 度 とすると、vc' は、
vc' = 3.0 × 1.0 × ( cos2(30) / (1 + 3 × cos2(30) ) ) = 0.6923 [m/sec]
上記のような棒のモデルを、Impact FEM 用に作成し、同様な条件で、速度 vc を与え、壁面から跳ね返りがないように衝突させてみた。

Fig.3 壁面に接地後の様子

Impact FEM は陽解法プログラムであるので、解が振動しているが、速度値 vc' は、大体 0.701 [m/sec] の値に収束している。理論式で得られた数値との差異は、1.26 [%] で、かなり近い値が得られた。
Impact FEM では、剛体が定義された節点郡に対して、さらに境界条件としての拘束などを与えることが困難なため、棒は、十分剛と思われる程度の剛性を定義した弾性体とした∗1。そのため、棒自体の変形によって、若干のエネルギ散逸(変形エネルギ散逸)が起こる。また理論式では、棒の幅寸法について無視したとことで、三角関数を用いた成分計算のときの角度値が、真値とは少しずれている。これらの要因から、理論式とは少し数値がずれているものと考える。
∗1 : ここでは、致し方なく十分剛な弾性体を使用したが、十分剛な弾性体を、陽解法で計算するモデル内に含むと、安定時間増分 Δt を無意味に縮小させ、計算コストを増大させるので、あまり好ましくない方法ではある。また、剛に近い弾性体による、妙な高周波ノイズを結果に含むことにもなる。なまじ、陰解法より、実際の現象に忠実な解法であるため、実際には存在し得ない
剛体などという定義の扱いに、特に注意しないといけない気がする。

